Quali fattori influenzano il raccolto giornaliero di miele?
di Daniele Besomi
Abstract: Durante un flusso nettarifero, il raccolto di miele varia —e anche parecchio— di giorno in giorno, essenzialmente a seconda delle variabili meteorologiche che infuenzano la produttività delle piante e/o la capacità di volare delle api. In questo articolo si esaminano alcuni dei fattori che hanno determinato le fluttuazioni nel raccolto estivo del 2025, identificando come statisticamente significative la velocità del vento, la luminosità solare, la pioggia e l'umidità assoluta.
Introduzione: la variabilità del raccolto giornaliero
Qualsiasi apicoltore che disponga di una bilancia che misura il peso di una o più arnie si è certamente accorto che, durante un flusso nettarifero, l'accrescimento di peso non è uguale giorno per giorno, ma è soggetto a una certa variabilità. Questo si vede dal grafico che riporta l'aumento di peso giornaliero di 5 arnie durante il raccolto di tiglio e castagno nell'estate 2025, calcolato come differenza tra il valore massimo registrato nella giornata (solitamente verso le 21:30 di ciascun giorno, cioè immediatamente dopo il rientro di tutte le bottinatrici e prima che il peso inizi a calare in seguito all'azione ventilatrice delle api per asciugare il nettare raccolto) e il corrispondente punto di massimo del giorno precedente. Le bilance hanno cominciato a salire il 14 giugno, in modo irregolare ma con una tendenza chiaramente riconoscibile; l'apporto giornaliero di nettare è cresciuto fino al 24 giugno, poi ha cominciato a calare diventando negativo dal 6 luglio, giorno in cui la perdita di peso dovuta all'essicazione del miele e al consumo delle api ha superato l'importazione di nettare.
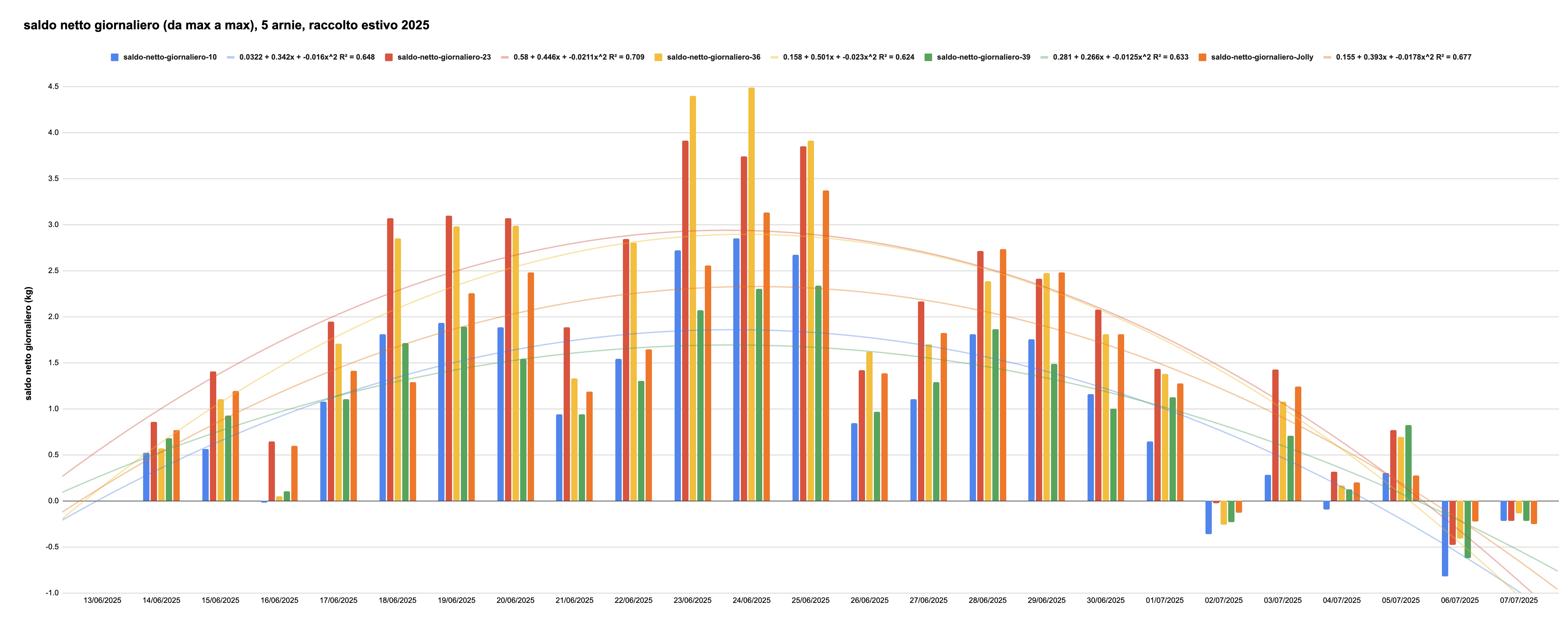
Figura 1: apporto netto giornaliero di nettare, raccolto estivo 2025
L'andamento generale è facilmente spiegabile: inizialmente solo poche piante sono fiorite, e solo parzialmente. Col passare dei giorni la fioritura continua ad aumentare, fino a quando i primi alberi cominciano a perdere i fiori. Da quel momento, il numero di alberi in fiore inizia a diminuire, fino alla fine della fioritura. Nel caso illustrato, si sono sovrapposte tre fioriture, ciascuna con il medesimo andamento: al miglioramento delle condizioni meteo il 14 giugno le api hanno potuto approfittare della fioritura del rovo, che a quel momento era verso il suo culmine; il castagno è fiorito il 19 giugno, mentre i primi tigli hanno schiuso i fiori a partire dal 26 giugno. Il tutto è complicato dal fatto che le api possono anche spostarsi più in alto o più in basso rispetto alla postazione, e dunque allungare il raccolto di qualche giorno rispetto alle date specifiche di inizio e fine fioritura alla quota esatta della postazione.
Il grafico mostra anche che la capacità delle colonie di raccogliere il nettare disponibile non è la medesima: al culmine, le due colonie più "forti" hanno raccolto circa il doppio rispetto alle due colonie relativamente più deboli, mentre la quinta colonia ha avuto un andamento intermedio rispetto ai due gruppi precedenti—peraltro con una partenza a rilento ma un finale in crescita.
Scopo e strumentazione
Lo scopo di questo articolo è di riflettere sulle deviazioni rispetto all'andamento generale, che nella figura 1 è riassunto approssimativamente (v. più avanti) dalle parabole che interpolano i dati di ciascuna arnia. Alcuni dati giornalieri sono decisamente al di sopra della parabola, mentre altri sono chiaramente minori dell'andamento tendenziale. L'obiettivo è di confrontare queste differenze con i dati meteo, raccolti tramite una centralina dedicata. Non si discute, invece, la causa dell'abbondanza o meno del flusso nettarifero —ovvero, l'ampiezza delle parabole rovesciate della figura 1, cioè se l'annata sia particolarmente buona o scarsa: qui sarà preso come un dato del problema della varianza attorno a quelle parabole.
I dati fisiologici delle colonie (peso, temperatura e umidità interni) sono raccolti tramite sensori beepro. La centralina meteo (velocità del vento, pioggia e intensità luminosa) è stata prodotta ad hoc da Beicalab; l'irradiazione solare è misurata anche tramite la produzione dell'impianto fotovoltaico collocato a pochi metri di distanza dalle arnie. I dati ambientali (temperatura e umidità) sono raccolti tramite sensori della Sensirion. Tutti gli strumenti registrano i dati ogni 2 minuti, salvo l'impianto fotovoltaico che rende i dati giornalieri.
L'apiario si trova a 900 metri di quota, nelle prealpi ticinesi.
Perché i dati meteo?
Abbiamo visto dalla figura 1 che vi sono differenze tra quanto ciascuna arnia riesce a raccogliere, non solo nell'arco dell'intero periodo (chi coglie di più, chi coglie meno, rappresentato dall'altezza delle parabole interpolanti) ma anche giorno per giorno. Tuttavia, in generale, sembrerebbe che quando una colonia raccoglie molto rispetto alla propria media anche le altre tendano a fare lo stesso. È necessario esaminare se prevalgano le individualità (e in tal caso significherebbe che le variazioni siano da attribuire principalmente alle specificità di ciascuna colonia) oppure se prevalgano le uniformità (e in tal caso dovremmo attribuire la componente principale delle variazioni a fattori in comune a tutte le colonie).
Una prima visualizzazione si trova nella figura 2, che riporta la temperatura esterna (linea grigia) e rappresenta il raccolto netto delle 5 colonie sotto esame (il dato è ottenuto calcolando l'incremento di peso a partire dal punto di massimo del 13 giugno, cioè il giorno precedente l'inizio del raccolto, sottraendo il peso dei melari man mano che venivano aggiunti).
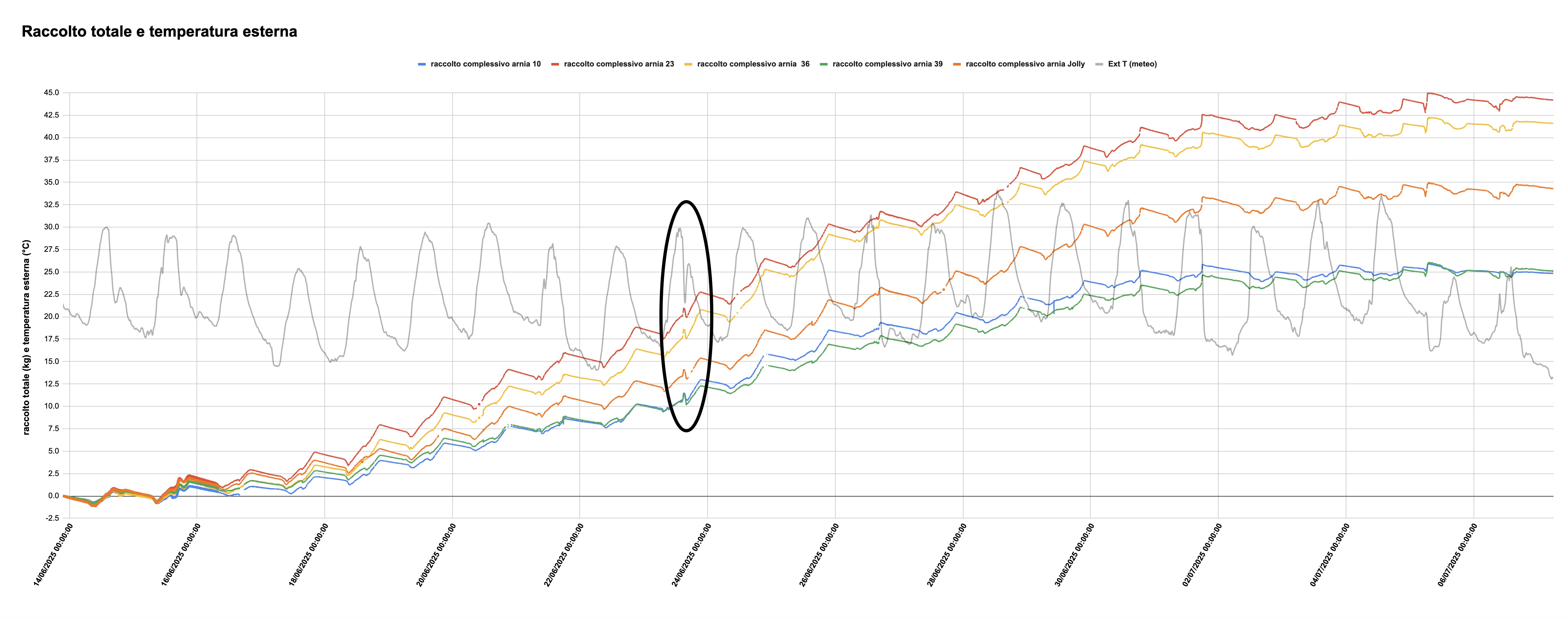
Figura 2: Raccolto netto totale e temperatura esterna durante il raccolto estivo 2025
A una prima occhiata, si percepisce che l'andamento delle curve che rappresentano il raccolto delle cinque arnie procede con un certo parallelismo. Questo è particolarmente evidente in corrispondenza del calo di temperatura nella parte evidenziata del grafico. Un ingrandimento, con qualche dato meteo aggiuntivo, è particolarmente illuminante.
La figura 3 rappresenta i dati relativi al raccolto del 22, 23 e 24 giugno, e i valori della temperatura (linea grigia), precipitazioni (linea blu), e luminosità solare (linea gialla, scala di destra). La curva della luminosità solare ci dice che mentre il 22 e il 24 giugno il tempo è stato bello con pochi e brevi passaggi nuvolosi, il 23 giugno è stato caratterizzato da frequenti passaggi nuvolosi con un oscuramento quasi totale alle 14:52; poco dopo, alle 14:58, ha iniziato a piovere. La temperatura è calata da quasi 30° a 21.5°C. In corrispondenza del fenomeno piovoso, il peso delle arnie mostra una gobba. 10 minuti prima che si raggiungesse la luminosità minima, il peso delle arnie ha cominciato a crescere: le api si sono accorte del temporale in arrivo e sono rientrate precipitosamente. Prima che iniziasse a piovere, il peso è cresciuto di 4-500 grammi per il numero di api in arrivo col loro carico di nettare, accrescendosi poi ulteriormente per il peso dell'acqua sui tetti delle arnie. Alla fine della pioggia è tornato rapidamente il sole (come indicato dalla luminosità tornata a livelli alti), e le api sono di nuovo uscite a continuare il loro lavoro, come evidenziato dalla diminuzione di peso —coadiuvata dall'evaporazione dell'acqua sui tetti e da quella assorbita dal legno di arnie e melari.
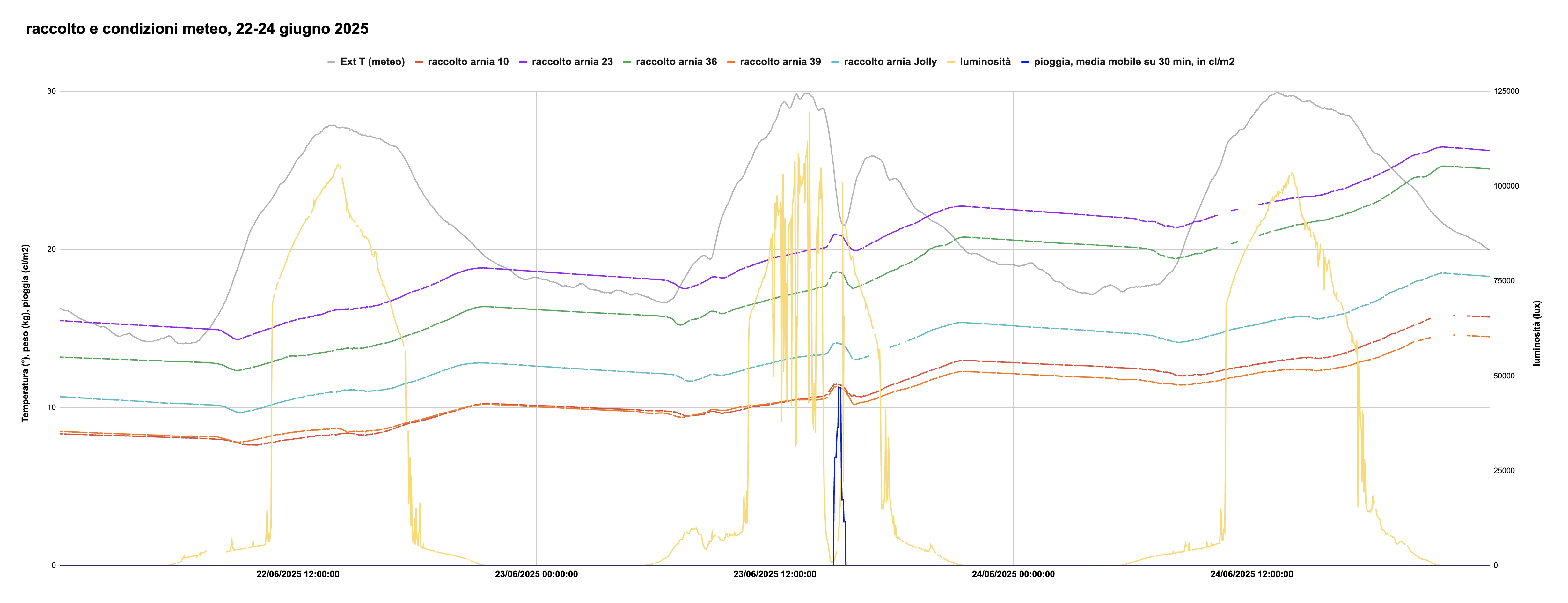 Figura 3: Condizioni meteo (temperatura, luminosità e pioggia) e andamento del raccolto, 22-24 giugno 2025
Figura 3: Condizioni meteo (temperatura, luminosità e pioggia) e andamento del raccolto, 22-24 giugno 2025
Per quanto questi parallelismi percepibili a colpo d'occhio siano molto suggestivi, per poter concludere a favore o contro la tesi dell'uniformità dell'andamento dei raccolti delle cinque colonie è però necessaria un'analisi della correlazione tra i rispettivi movimenti. Si tratta di esaminare cosa succede al raccolto giornaliero di ciascuna arnia rispetto a quello di un'altra aria presa come riferimento. Questo è quanto fa la figura 4. Sull'asse orizzontale è indicato il raccolto giornaliero della colonia dell'arnia 10, mentre in verticale si legge il raccolto del medesimo giorno delle altre colonie.
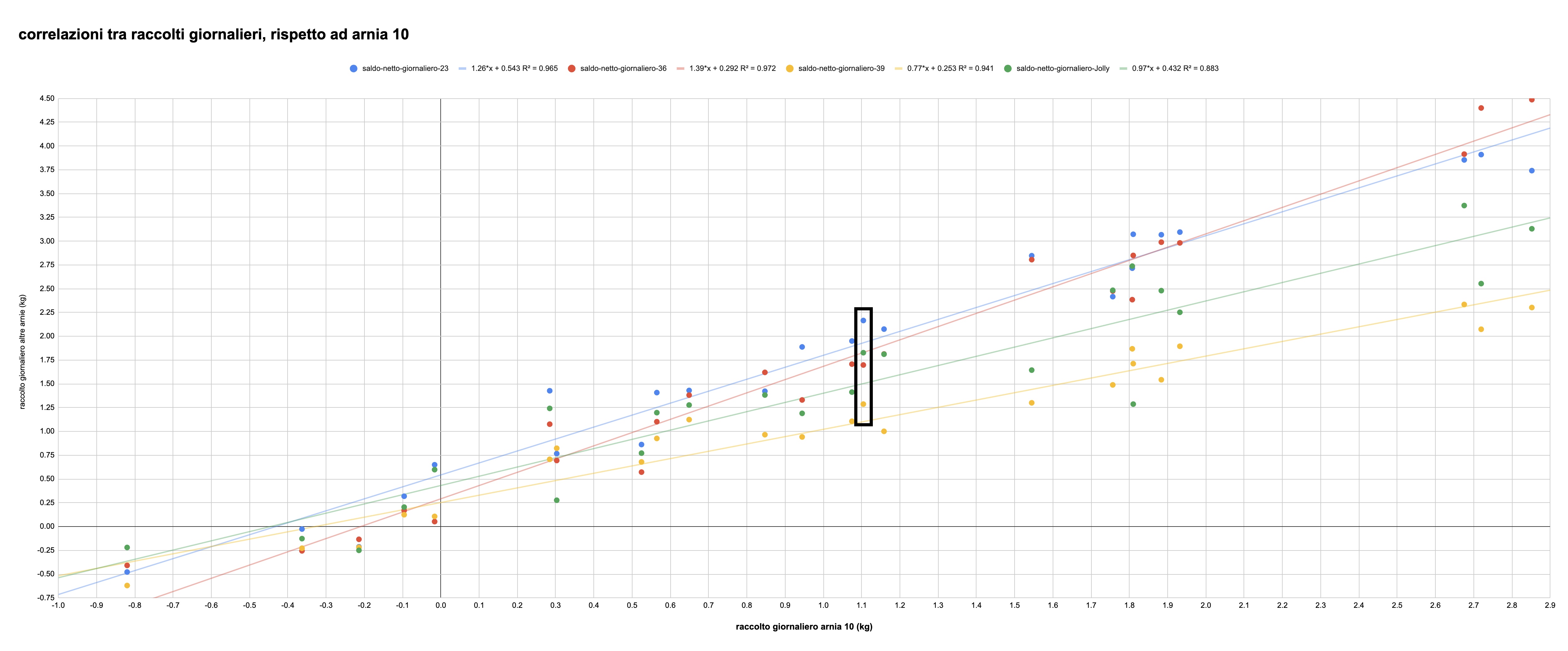
Figura 4: raccolto giornaliero di 4 arnie rispetto al raccolto giornaliero della quinta arnia (la numero 10). I dati si leggono come segue, prendendo l'esempio dei valori nel rettangolo nero: nel giorno in cui l'arnia 10 ha raccolto 1.1 kg (il valore sul'asse orizzontale) le altre colonie hanno raccolto: 1.3 kg (arnia 39, gialla); 1.7 kg (arnia 36, rossa); 1.83 kg (arnia Jolly, verde); e 2.17 kg (arnia 23, blu). Le linee rappresentano l'interpolante, la cui equazione è data nella legenda, assieme al rapporto di correlazione.
Il dato rilevante è che al crescere del quantitativo raccolto dall'arnia 10, cresce anche il raccolto delle altre arnie, nella proporzione media indicata dalla pendenza della linea retta che interpola i dati. Quanto bene le rette approssimino i punti specifici è indicato dal rapporto di correlazione R2 (indicato nella legenda), un numero che può assumere valori tra 0 (nessuna relazione statistica tra i dati) e 1 (relazione perfettamente proporzionale). Nel nostro caso i valori di tre delle arnie sono superiori a 0.94, mentre per la quarta arnia —quella denominata Jolly, che abbiamo visto in precedenza essere partita più lentamente delle altre ma aver poi accelerato— vale comunque 0.88. Cosa significa questo? I raccolti giornalieri delle cinque colonie si muovono all'unisono, crescono e diminuiscono tutte assieme in una proporzione quasi costante giorno dopo giorno (con la parziale eccezione dell'arnia Jolly). Per tutte le colonie, la correlazione tra gli incrementi giornalieri netti è statisticamente altamente significativa.
La variabilità del quantitativo di nettare raccolto giornalmente dipende dunque molto poco dall'individualità di ciascuna colonia (che determina comunque il valore assoluto di questa grandezza: le colonie nelle arnie 23 e 36 sono in grado di raccogliere più della Jolly, che a sua volta raccoglie più della 39, la quale invece è grossomodo equivalente all'arnia 10; l'indicazione quantitativa è data dai coefficienti delle rette interpolanti), ma dipende piuttosto da qualche fattore esterno comune a tutte loro. Il sospetto, ovviamente, è che questo fattore sia legato alla meteorologia.
Raccolto e ondate di calore
Prima di entrare nell'analisi dei diversi fattori che entrano nell'equazione è necessaria una riflessione specifica riguardante una singola variabile: la temperatura. Come si vede dalla figura 2, nel periodo del raccolto vi sono stati diversi giorni con temperature (all'ombra) di oltre 30°C. Ma molti degli alberi visitati dalle api avevano parte della chioma e dei fiori al sole, e le stesse api dovevano volare al sole almeno parte del loro percorso. In letteratura si trova l'indicazione che diverse piante, al di sopra di una certa temperatura (potenzialmente diversa per ogni specie), rallentano o addirittura cessano la produzione di nettare. Studi specifici, in effetti rilevano in un certo numero di casi una relazione a parabola rovesciata tra la produzione di nettare per fiore e la temperatura: se la temperatura è troppo bassa, la pianta non riesce a produrre nettare (cosa che spesso accade, per esempio, alla fioritura della Robinia pseudoacacia: a belle fioriture non corrisponde la produzione di nettare se la temperatura è inferiore a una certa soglia). La produzione aumenta man mano che cresce la temperatura esterna, ma oltre un certo punto comincia a diminuire, in particolare perché il calore diminuisce la disponibilità dell'acqua necessaria per produrre il nettare e favorisce un'eccessiva essicazione del nettare (che rende difficile raccoglierlo), e poi cessa completamente.[1] Per quanto riguarda il volo delle api, la questione è ancora aperta in letteratura. Studi recenti collocano la temperatura toracica ottimale delle api per il metabolismo del volo attorno a 39°C, cosa che si verifica quando la temperatura esterna si situa attorno a 32°. In tutto il periodo del raccolto, la temperatura ha superato 32°C —facendo entrare le api nella zona a rendimenti decrescenti nello sforzo di volo— per 1-4 ore al giorno in cinque delle giornate alla fine del raccolto, tra il 28 giugno e il 4 luglio. Questo non è probabilmente sufficiente a causare difficoltà rilevanti al volo delle api,[2] per cui possiamo pensare che il fattore predominante qui sia l'effetto della temperatura sulla capacità delle piane di produrre nettare, anziché la capacità delle api di raccoglierlo. In condizioni nelle quali la temperatura è più alta, però, il metabolismo del volo potrebbe essere seriamente disturbato, e occorrerebbe tenerne conto.
Il grafico in figura 5 riporta il raccolto del 2025 (misurato sull'asse verticale) in relazione alla temperatura massima esterna del giorno corrispondente (asse verticale):
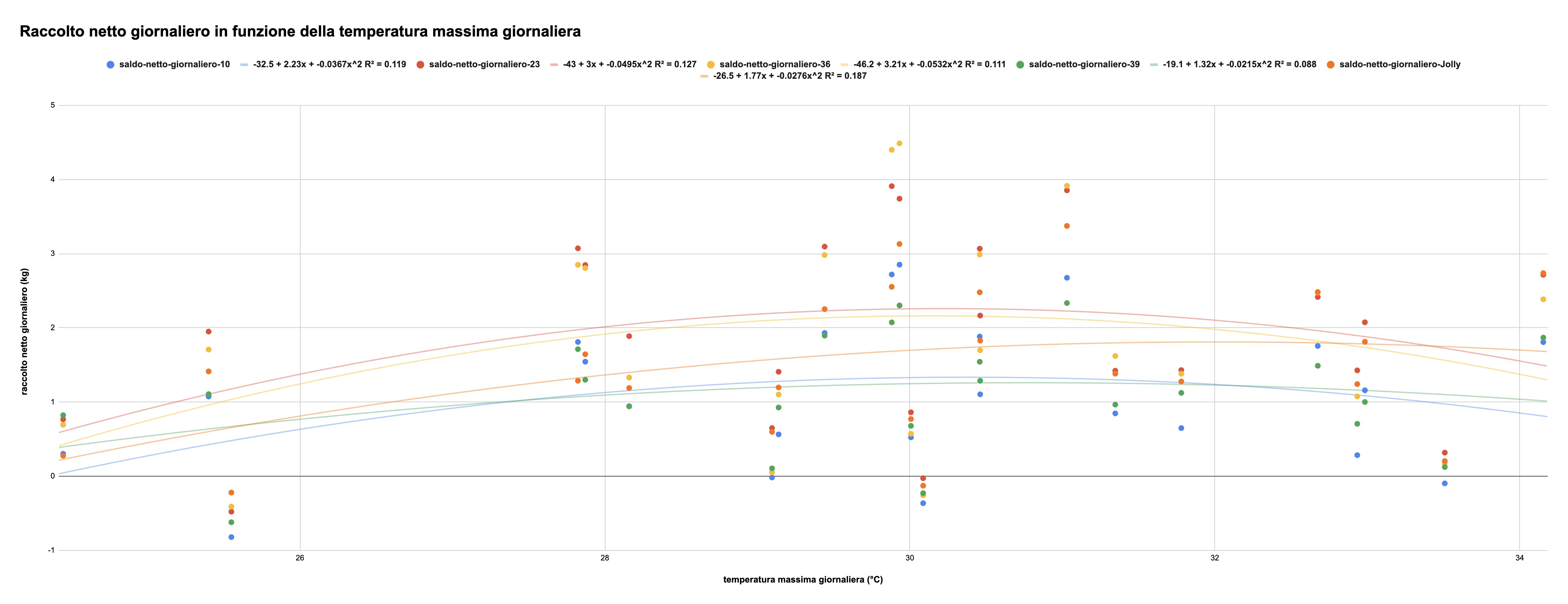
Figura 5: raccolto giornaliero delle 5 arnie (asse verticale, in kg) in corrispondenza della temperatura massima del giorno (asse verticale, °C)
La produzione di nettare di tiglio, castagno e rovo (le essenze principali raccolte dalle api) non sembra sia stata esplicitamente studiata in letteratura, e non abbiamo dunque un termine di paragone. Qui rileviamo che i dati sono disposti lungo una curva a parabola rovesciata, che comunque riflette le constatazioni relative ad altre piante: temperature massime inferiori a 26° e superiori a 32° non sembrano essere molto favorevoli al raccolto, mentre il massimo si ottiene a temperature comprese tra 29 e 31°C.
Misura della variabilità
Possiamo ora passare al problema che ci proponiamo di studiare, cioè esaminare se e come i fattori meteorologici influenzino le deviazioni del raccolto dal valore che mediamente possiamo aspettarci. In figura 1 avevo utilizzato una parabola come interpolante, non per qualche ragione logica o matematica ma semplicemente perché si trattava del tipo di curva tra quelle offerte dal foglio di calcolo (Googlesheets, ma varrebbe lo stesso con Excel) che meglio approssimava i valori concreti.[3] La variabile da 'spiegare' statisticamente è la deviazione tra i valori effettivi e la parabola interpolante: quali sono i fattori che determinano se in un determinato giorno le api raccolgono più o meno di quanto indicato dalla parabola?
L'approccio seguito consiste nello sviluppare dei modelli lineari che minimizzano la distanza tra i valori effettivi registrati empiricamente e retta stimata in base alle variabili scelte (minimi quadrati ordinari). Nel caso semplice in cui si intende confrontare l'andamento di una variabile con quello di una sola altra variabile, è la medesima procedura che usano i fogli di calcolo per determinare l'interpolante lineare, come fatto per esempio nella figura 4. L'equazione data in legenda tra arnia 10 (la base di confronto per tutte le altre) e l'arnia 23 (punti blu) ci dice:
il raccolto giornaliero dell'arnia 23 (y) = 1.26 volte il raccolto giornaliero dell'arnia 10 (x) + una costante (in questo caso =0. 543).
Quindi: se l'arnia 10 raccoglie 1.1 kg (il valore nel rettangolo nero), ci si aspetta che l'arnia 23 raccolga 1.26 * 1.1 kg + 0.543 kg = 1.929 kg. In realtà, nel giorno in cui l'arnia 10 ha raccolto 1.1 kg l'arnia 23 ha raccolto 2.2 kg, cioè più di quanto ci si aspettasse. La stima incorpora dunque degli errori, a volte per eccesso e a volte per difetto. La formula è costruita in modo tale da minimizzare la media del quadrato di questi errori.
Il problema che dobbiamo affrontare ora non è quello di analizzare le variabili una alla volta, ma di considerare congiuntamente le diverse componenti che concorrono alla spiegazione del fenomeno. Quali variabili? A priori, non lo so, ma si tratta di verificare se il raccolto in eccesso o in difetto rispetto alla media abbia a che vedere con il vento (valore medio durante il giorno? il massimo?); la temperatura esterna (la media? il massimo? il minimo? i minuti al di sopra di un certo valore?); l'umidità esterna (quella relativa? quella assoluta? valori medi, massimi o minimi, o al di sopra di una certa soglia?), la pioggia (il numero di minuti di pioggia? l'intensità?) e la luminosità (una media? il totale giornaliero?). La lista naturalmente non è esaustiva (v. discussione), ma questo sono le variabili di cui dispongo, e comunque sono alcune di quelle discusse in letteratura. Ho dunque provato, per ciascuna delle arnie, diverse combinazioni, alla ricerca di quelle che dessero dei risultati statisticamente significativi.
Lo strumento utilizzato per la modellistica e l'analisi statistica è il software open source Gretl.
Risultati
L'analisi di tutte e 5 le colonie mostra che le variazioni del raccolto giornaliero attorno al valore medio rappresentato dalla parabola della figura 1 è molto significativamente sensibile a:
- velocità massima del vento nel giorno in questione, misurata dall'anemometro dell'impianto meteo. In alternativa, si possono usare le massime diurne, con parametri e significatività complessivi abbastanza simili.
- l'intensità della luce solare durante l'intera giornata, calcolata in due modi (che alla fine risultano sostanzialmente equivalenti): il primo è ottenuto sommando le intensità misurate dallo strumento meteo ogni 2 minuti. Il valore è dunque sensibile sia all'intensità misurata per ciascun intervallo che al numero di minuti di soleggiamento. Quest'ultima componente del risultato, però, varia pochissimo nel periodo considerato, a cavallo del solstizio estivo. Il risultato giornaliero è influenzato sia dalla limpidezza dell'aria che dai passaggi nuvolosi). Il secondo, meno artificialmente, è ottenuto utilizzano i dati giornalieri registrati dal mio impianto fotovoltaico.
- la pioggia (misurata in mm al giorno dal pluviometro dello strumento meteo o, alternativamente —di nuovo senza mutare sensibilmente il risultato— in base al numero di minuti in cui ha piovuto).
Per quanto riguarda i valori di temperatura e umidità esterni, tutte le colonie salvo una (la numero 23) si sono dimostrate significativamente sensibili anche al valore dell'umidità assoluta (data dai sensori Sensirion), più precisamente al numero di minuti in cui l'umidità assoluta è stata superiore a 15g/m3. La variabilità del peso della colonia 23, invece, oltre a pioggia, vento e luminosità solare come le altre, è sensibile in modo significativo anche al numero di minuti al giorno in cui la temperatura è superiore a 25°C.
I dati meteo e del raccolto (arnia 36, inclusa la parabola interpolante) sono rappresentati nella figura 6:
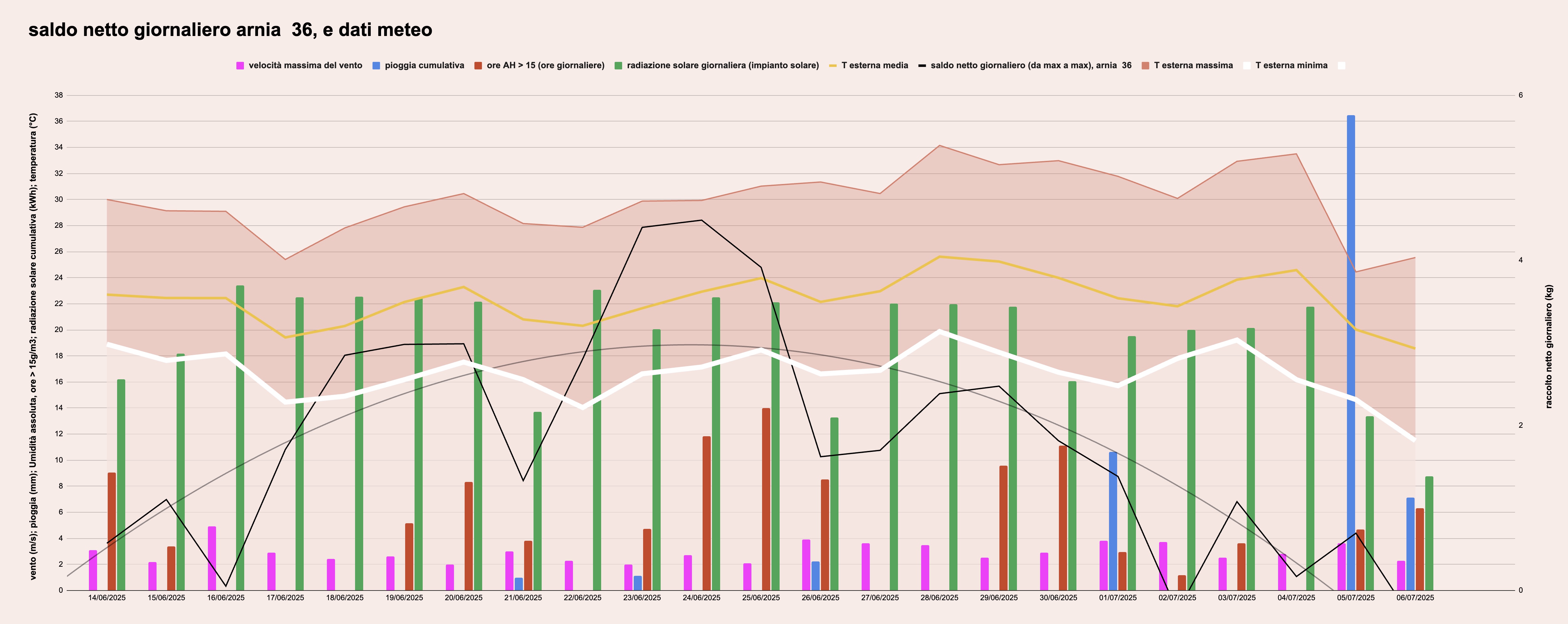
Figura 6: raccolto netto giornaliero dell'arnia 36 (linea nera + parabola interpolante, scala di destra), e dati meteo (colonne, scala di sinistra): la velocità massima giornaliera del vento, la pioggia cumulata nella giornata, il numero di ore in cui l'umidità assolta supera 15 g/m3. Le temperature sono rappresentate nella fascia più scura, tra le massime e le minime del giorno, all'interno della quale c'è la linea della temperatura media giornaliera.
La generica equazione corrispondente a questo modello con 4 variabili è
y = ax1 + bx2 + cx3 + dx4 + e
Si tratta di una linea retta in uno spazio a 5 dimensioni:
y è la stima della variabile dipendente, quello che cerchiamo di "spiegare" —che nel nostro caso è la deviazione del raccolto giornaliero rispetto alla parabola.
x1, x2, x3 e x4 sono i valori effettivamente registrati dalle variabili indipendenti, quelle chiamate a "spiegare" statisticamente i valori di y.
Infine, i parametri a, b, c, d, e sono calcolati in modo tale da minimizzare la distanza tra i valori effettivamente misurati dalla variabile dipendente (cioè il valore effettivo della deviazione del raccolto dalla media) e la retta che porta alla stima y. In pratica, il modello mira a calcolare la stima che meglio rappresenta la realtà (misurata in termini di distanza dei dati effettivi dalla retta risultante dalla stima), assumendo che la linea retta dia quella che meglio rappresenta il fenomeno in questione. L'analisi statistica permette di valutare se i coefficienti a, b, c, d ed e sono statisticamente significativi, cioè se le variabili x1, x2, x3 e x4 effettivamente influenzano il fenomeno sotto esame oppure se la relazione tra queste variabili è un risultato casuale.
L'interesse di questa modellistica non sta solo nel permettere di individuare le variabili probabilmente rilevanti, ma anche di stimarne l'impatto sul fenomeno, sia qualitativamente (se, per esempio, aumenta il vento, il raccolto aumenta o diminuisce?) che quantitativamente (rispondendo alla domanda: se la velocità del vento aumenta di 1 m/s, quanti kg di raccolto in più o in meno possiamo aspettarci?)
Veniamo ora ai risultati concretamente trovati dal nostro modello, prendendo come esempio l'arnia 36 (le tabelle complete sono riportate in appendice). L'equazione di stima dei parametri ha portato al seguente modello:
deviazione del raccolto giornaliero dalla media (in kg) = -0.78306*velocità max del vento + 0.104627 *intensità luminosa complessiva +0.0567591*mm di pioggia + 0.00110273*n° minuti in cui l'umidità assoluta > 15g/m3 + una costante (=-0.227242)
Quale rilevanza quantitativa e qualitativa ha questo risultato? Esaminiamo uno a uno i coefficienti delle variabili in gioco, a partire dal vento. Si tratta di un risultato molto robusto, con alta significatività statistica, qualitativamente coerente con quanto ci si aspetterebbe, e abbastanza uniforme nei modelli per le diverse colonie (i valori oscillano tra -0.35 e -0.91, e sono molto significativi per tutti i modelli —vedi Appendice per i modelli di questa e delle altre colonie). Il segno negativo ci dice che più vento c'è, meno le api riescono a raccogliere. Il valore del coefficiente, 0.78, significa che per ogni aumento del vento di 1 m/s il raccolto diminuisce rispetto alla parabola di 0.78 kg (a parità delle altre condizioni, naturalmente). Si tratta di un quantitativo molto importante, coerente con altri risultati discussi in letteratura. Il suo effetto è attribuito al fatto che il vento prosciuga il nettare dei fiori[4] e che rende difficile il volo degli insetti.[5]
L'intensità luminosa complessiva, misurata in kWh prodotti dall'impianto fotovoltaico ha un ruolo quantitativamente importante —anche grazie al fatto che c'è qualche correlazione, seppure non robustissima, con i valori della temperatura. Il segno del coefficiente è positivo, ad indicare che quanto più intensa è la luce solare, tanto maggiore il raccolto potenziale. Ogni kWh in più prodotto dall'impianto solare si traduce in un raccolto aggiuntivo, sempre rispetto alla parabola interpolante e a parità di valori delle altre variabili, di 104 grammi. Poiché la produzione di energia in quel periodo oscillava tra i 20 e 23.3 kWh (considerando solo i giorni di bel tempo, con valori verso il basso fino a 13 nei giorni con pioggia o copertura nuvolosa) le variazioni di irradiazione solare nei giorni di bel tempo sono responsabili di fluttuazioni fino a 312 grammi al giorno attorno alla parabola che rappresenta la media.
Il coefficiente legato alla pioggia è invece più problematico, pur essendo statisticamente significativo. Ci si aspetterebbe, infatti, che nei giorni di pioggia le api raccolgano meno nettare. Tuttavia, il coefficiente della variabile è positivo. Questo paradosso è solo apparente: la bilancia in realtà misura l'aumento di peso, non un aumento del raccolto. Nei giorni di tempo secco fa poca differenza, ma nei giorni piovosi l'effetto diventa rilevante. La pioggia, spesso caduta nel pomeriggio,[7] inumidisce coperchio e pareti dell'arnia, che quindi diventano più pesanti e lo restano, in qualche misura, fino a sera.[8]
I minuti in cui l'umidità assoluta supera 15 g/m3 oscillano tra 0 e 840 (riportati in ore in figura 6: tra 0 e 14). Con il coefficiente di 0.11, questo potrebbe comportare oscillazioni di quasi 1 kg rispetto alla media (sempre assumendo la costanza degli altri fattori); anche questo fattore è dunque rilevante e statisticamente significativo.
Applicando il modello ai dati concreti si ottiene la stima del raccolto che la colonia nell'arnia 36 avrebbe dovuto fare se i 4 fattori elencati (vento, pioggia, umidità assoluta e irradiazione solare) fossero le uniche variabili ad influenzare il raccolto. Ma ovviamente così non è. La stima, dunque, include degli errori. La figura 7 riporta i valori effettivamente misurati del raccolto (blu), la stima del modello (rosso), e gli errori di stima giorno per giorno (barre gialle):
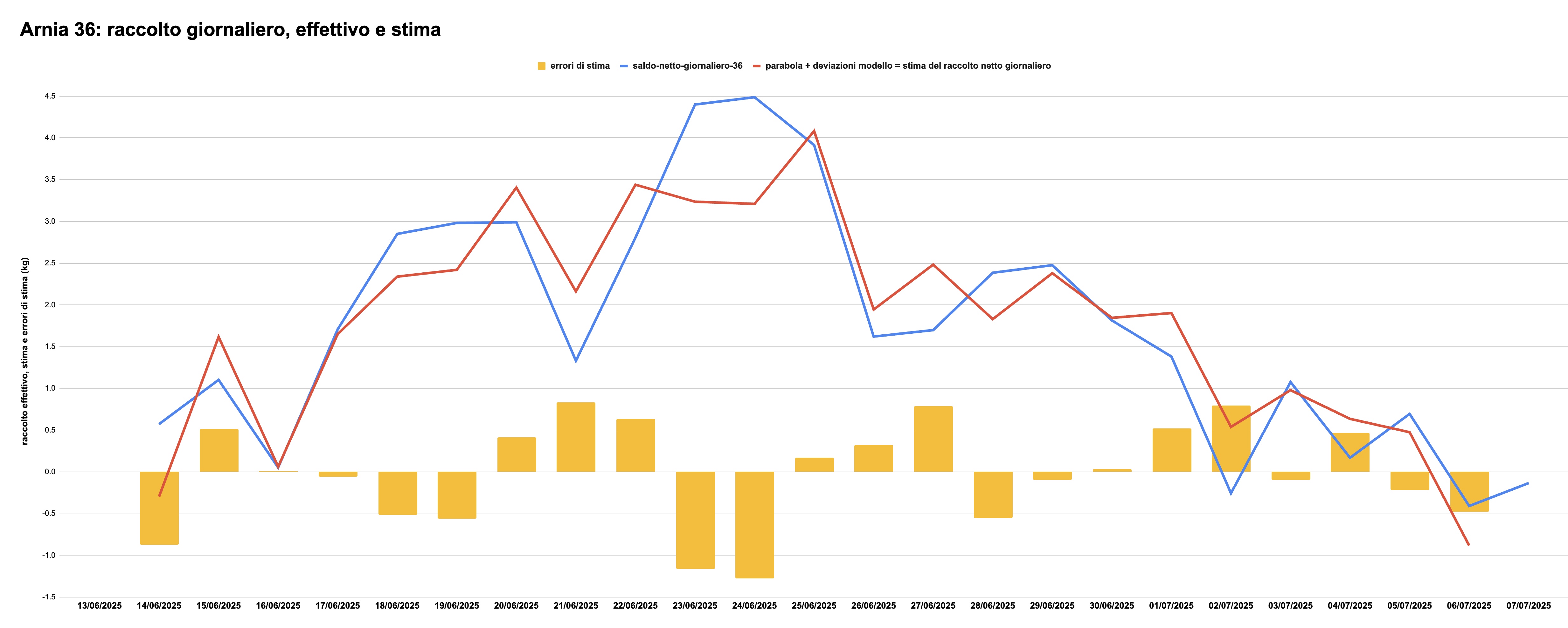
Figura 7: valori effettivi, valori stimati e errori di stima relativi all'arnia 36
Il valore medio del raccolto effettivo è di 1.74 kg al giorno; il valore medio della stima prodotta dal modello è di 1.80 kg al giorno (dunque piuttosto simile), e la media degli errori di stima (verso l'alto o verso il basso) è di circa 500 grammi. Alcuni di questi errori sono molto grossi. Il 23 e 24 giugno, per esempio, il modello si aspettava una crescita di oltre 1 kg minore di quanto non sia effettivamente successo, mentre al contrario in corrispondenza dei raccolti scarsi del 21 e 27 giugno e del 2 luglio il modello ha peccato di ottimismo.
Discussione
Gli errori di stima del modello non sono casuali. Se si mettono in relazione gli errori di stima con la deviazione del raccolto giornaliero dalla parabola, risulta che i valori sono correlati: tanto più grande è la deviazione dalla parabola (verso l'alto o verso il basso) tanto maggiore è l'errore di stima, nella direzione opposta (figura 8). Per ogni kg di eccesso di produzione rispetto alla parabola, la stima prevede una deviazione di circa la metà rispetto all'effettivo:
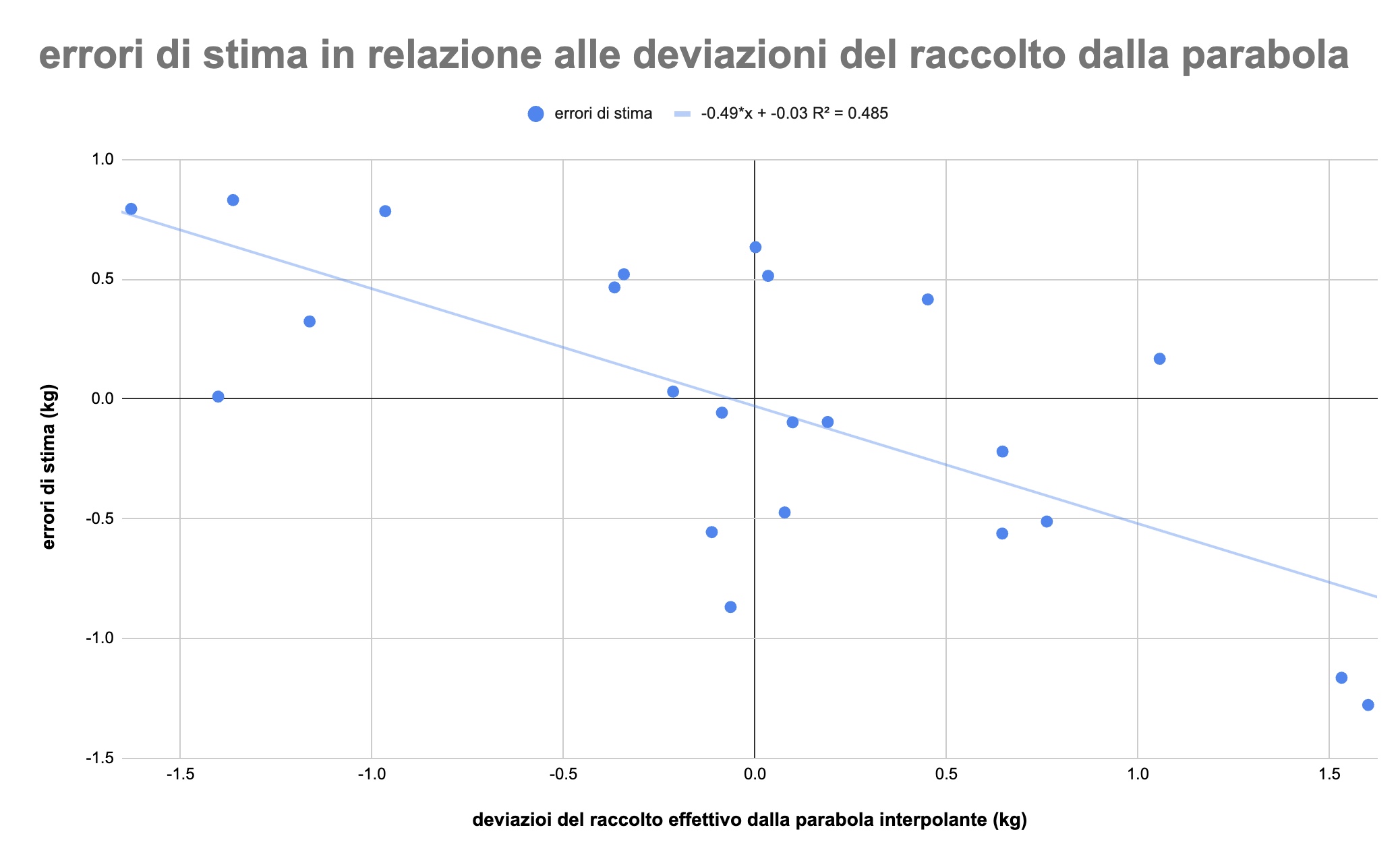
Figura 8: Correlazione tra lo scarto del raccolto effettivo rispetto alla parabola e i corrispondenti errori di stima: più è grande la deviazione dalla parabola, verso l'alto o verso il basso, tanto maggiore è l'errore di stima.
Insomma, il modello sottovaluta le deviazioni verso l'alto e sopravvaluta le deviazioni verso il basso: i fattori incorporati nel modello spiegano dunque solo parte dei picchi e delle valli della figura 7 (la curva rossa delle stime ha oscillazioni più contenute rispetto alla curva blu dei valori effettivi), ma non sanno cogliere l'interezza degli eccessi o dei difetti di produzione rispetto alla media. Nel modello manca qualcosa che spieghi i comportamenti estremi, ma d'altra parte i fattori inclusi nel modello riescono a rendere conto almeno della direzione del cambiamento.
Non bisogna dunque prendere molto sul serio i valori numerici associati a questo specifico modello. Abbiamo a che fare con un sistema molto complesso, nel quale interagiscono (e in modo non lineare) almeno due ordini di considerazioni: quello che fanno le piante, e quello che fanno le api. Entrambi sono certamente soggetti all'influenza di breve periodo delle condizioni metereologiche giornaliere (quanto si è cercato di includere in questo semplice modello), ma possono anche essere affetti da altre variabili ambientali o dalle condizioni di qualche giorno prima (per esempio: di quanto tempo hanno bisogno le piante per recuperare i danni di un improvviso calo di temperatura durante un raccolto?).[9]
Tra i dati ambientali che in letteratura sono stati trovati di qualche rilievo bisogna senz'altro includere temperatura, umidità relativa, inquinamento ambientale (particolato, ozono ecc.), copertura nuvolosa, pressione atmosferica, cariche elettriche. Alcune di queste grandezze sono correlate tra loro.[10] L'umidità, in particolare, sia relativa che assoluta, è in parte legata alla temperatura: questa determina sia l'evaporazione che la condensazione del vapore, aggiungendo e sottraendo vapore acqueo all'aria; vapore la cui solubilità nell'aria dipende anch'esso dalla temperatura. Può dunque apparire strano che la temperatura non figuri tra le variabili che dano risultati significativi nel nostro modello. Tuttavia, se invece di analizzare le deviazioni dalla media si provasse a cercare i fattori che determinano il raccolto netto giornaliero, per tutte le colonie la temperatura diventa una variabile significativa anche nel nostro modello, assieme alla velocità massima giornaliera del vento (non, però, l'umidità).
Un altro fattore su cui si sta lavorando è la temperatura del suolo, in particolare in relazione alla temperatura di superficie. È in corso uno studio italiano, che monitora però anche dati internazionali (dovrebbero esserci anche quelli del mio apiario, se non fosse che una defaillance tecnica ha impedito la raccolta e la trasmissione dei dati proprio durante il periodo del raccolto), che poggia sull'idea che le complesse relazioni tra piante e insetti non siano sufficienti a spiegare la produzione di nettare, in quanto una parte rilevante del fenomeno avviene sotto terra, con le intricate relazioni tra parte aerea delle piante e rizosfera, in un rapporto a tre che coinvolge anche gli impollinatori.[11] Sarà interessante vedere i risultati, così come occorrerà confrontare i dati qui raccolti con quelli che si registreranno nei prossimi anni —possibilmente anche col contributo dei dati del suolo.
Note e riferimenti bibliografici
[1] Per esempio, Takkis e colleghi esaminano la produzione di nettare per fiore di una decina di piante mediterranee, osservando che quelle che subiscono maggiormente le limitazioni dovute alla temperatura sono quelle che fioriscono a tarda primavera o in estate (Takkis K, Tscheulin T and Petanidou T (2018) Differential Effects of Climate Warming on the Nectar Secretion of Early- and Late-Flowering Mediterranean Plants. Front. Plant Sci. 9:874. doi:10.3389/fpls.2018.00874). Plos et al. esaminano invece 4 specie erbacee centroeuropee (le misurazioni sono avvenute in Germania) considerando sia la produzione e la qualità del nettare che l'attività degli impollinatori rispetto a due variabili: la temperatura e la luminosità. I risultati sono meno univoci dei precedenti, anche se al crescere della temperatura la quantità di nettare prodotto tende a diminuire mentre la concentrazione tende ad aumentare; una delle 4 specie nel complesso vede diminuire la massa zuccherina prodotta al crescere della temperatura, le altre non sono molto influenzate. L'intensità della radiazione solare influenza solo alcune piante e non (o meno) altre. Anche per quanto riguarda il numero di visite ai fiori da parte degli impollinatori i risultati sono variabili: al crescere della temperatura, due delle specie vegetali mostrano un andamento a parabola rovesciata (fino a una certa temperatura, il numero di visite cresce; oltre quella soglia, il numero decresce), mentre l'intensità luminosa influenza significativamente le visite a una sola specie vegetale (Carolin Plos, Niklas Stelbrink, Christine Romermann, Tiffany M. Knight e Isabell Hensen,Abiotic conditions affect nectar properties and flower visitation in four herbaceous plant species , Flora 303, 2023, https://doi.org/10.1016/j.flora.2023.152279). Chabert e colleghi rilevano che la produzione di massa zuccherina dei fiori individuali di girasole cresce al crescere della temperatura ma solo fino a 32°C, dopo di che diminuisce molto rapidamente: v. figura 9(Stan Chabert, Christopher Sénéchal e altri, Effect of environmental conditions and genotype on nectar secretion in sunflower (Helianthus annuus L.), Oilseeds & fat Crops and Lipids (OCL) 27:51, 2020).
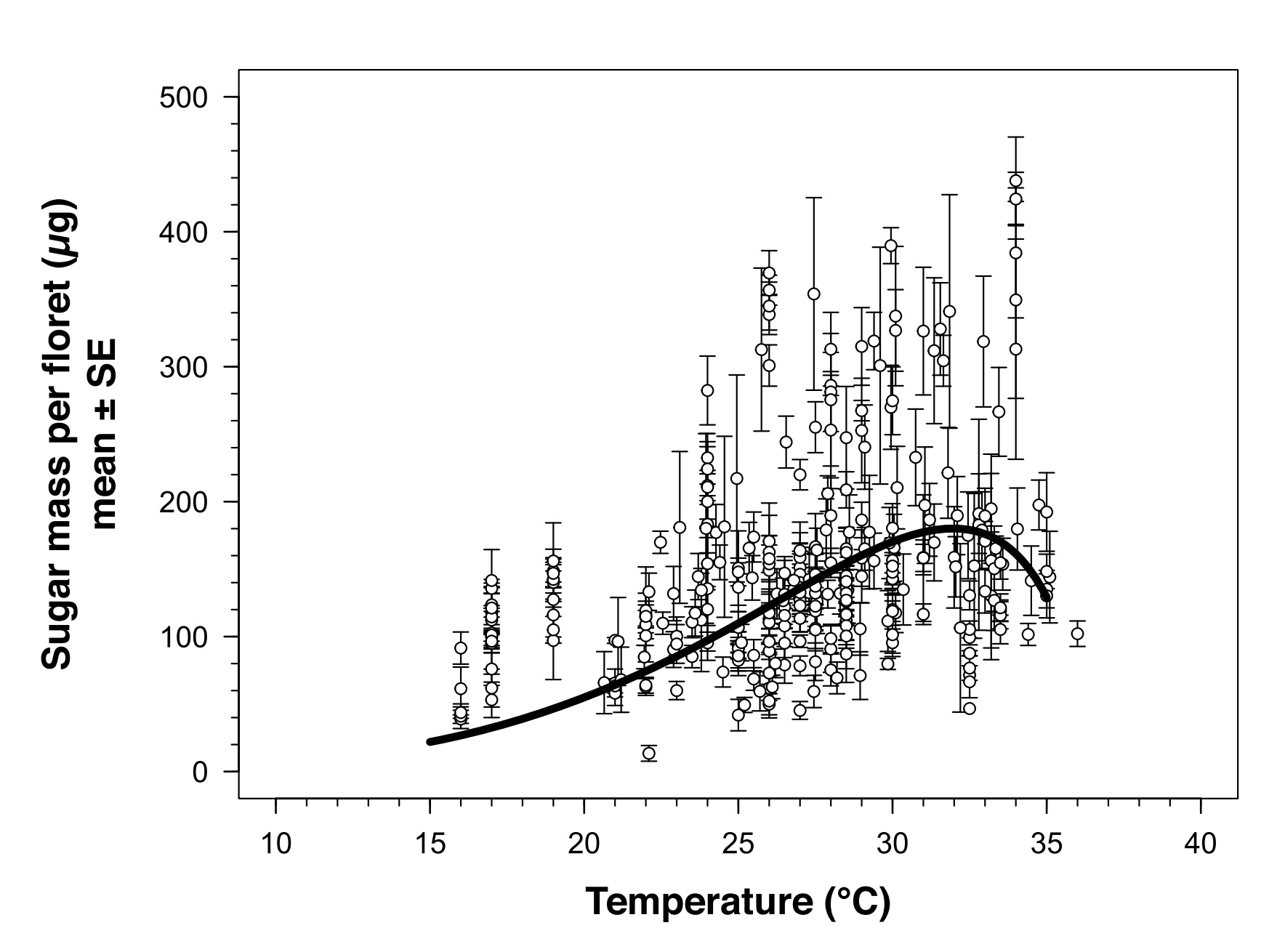
Figura 9: relazione tra la quantità di zucchero prodotta da ciascun fioredi girasole rispetto alla temperatura ambientale (da Chabert et al., citato)
[2] Jordan R. Glass e Jon F. Harrison, A thermal performance curve perspective explains decades of disagreements over how air temperature affects the flight metabolism of honey bees, Journal of Experimental Biology (2024) 227, jeb246926. doi:10.1242/jeb.246926
[3] La forma matematicamente precisa della parabola è arbitrariamente specifica, e non è detto che approssimi veramente bene il comportamento dei dati. Ho dunque provato anche una versione alternativa che evitasse di essere così specifica. Ho calcolato per ciascuna serie di incrementi netti di peso due sorte di curve di inviluppo, una superiore e una inferiore, che tra loro racchiudono tutti i dati relativi a ciascuna arnia, e ho calcolato una media tra loro. Le curve sono calcolate in questo modo: si determina un intervallo di tempo, entro il quale si calcolano rispettivamente il valore massimo e minimo tra i dati; poi si sposta avanti questo intervallo, e si ricalcolano massimi e minimi, e così via fino alla fine. Si applica poi un fattore di arrotondamento per evitare curve troppo spigolose. Il risultato saranno le (approssimative) curve di inviluppo superiore e inferiore. Il termine di riferimento usato è la media tra questi due valori. Ho provato la modellistica che si descriverà in seguito sia sulle deviazioni dei dati effettivi dalla parabola che da questa media. I risultati sono estremamente simili, sia in termini delle variabili che risultano essere statisticamente significative (identiche nelle due alternative) che in termini dei valori numerici dei coefficienti. Per semplicità espositiva, nel seguito utilizzerò la parabola come linea di riferimento.
[4] v. per esempio Mauro Pinzauti. The influence of the wind on nectar secretion from the melon and on the flight of bees: the use of an artificial wind-break, Apidologie, 1986, 17 (1), p. 67, con riferimento ai fiori di anguria. Per altre fioriture, non è stata trovata nessuna correlazione significativa tra vento e produzione di nettare (p.es. nelle cipolle: Erin M. Silva, Bill B. Dean, Larry Hiller, Patterns of Floral Nectar Production of Onion (Allium cepa L.) and the Effects of Environmental Conditions, J. AMER. SOC. HORT. SCI. 129(3):299–302. 2004)
[5] Vincens e Bosch, esaminando un frutteto di meli, hanno constatato che, una volta raggiunto un minimo di radiazione solare, tra le variabili meteorologiche il vento è il fattore più significativo nel determinare, limitandolo, il numero di visite ai fiori (Narcís Vicens e Jordi Bosch, Weather-Dependent Pollinator Activity in an Apple Orchard, with Special Reference to Osmia cornuta and Apis mellifera (Hymenoptera: Megachilidae and Apidae), Environmental Entomology, 29(3) 2000, pp. 413-420). Hennessy e coautori hanno misurato l'intensità e la durata delle visite a fiori sottoposti a diverse intensità di vento artificialmente creato, spiegando il risultato di Vincent e Bosch con la constatazione che con l'intensificarsi del vento le api esitano maggiormente a ripartire, diminuendo così il numero di visite; nel caso di origno e lavanda, per esempio, un aumento del vento da 0-1 m/a a 2.5-3.5 m/s comporta una riduzione del 36-38% delle visite ai fiori (Georgia Hennessy, Ciaran Harris, Charlotte Eaton, Paul Wrigh, Emily Jackson, Dave Goulson, Francis F. L. W. Ratnieks, Gone with the wind: effects of wind on honey bee visit rate and foraging behaviour, Journal of Animal Behaviour 161, 2020; Georgia Hennessy, Ciaran Harris, Lucien Pirot , Alexandra Lefter, Dave Goulson, Francis L. W. Ratnieks, Wind slows play: increasing wind speed reduces flower visiting rate in honey bees, Animal behaviour 178, 2021). Pinzauti, al contrario, riteneva invece che la difficoltà delle api consistesse nell'atterrare sul fiore (Mauro Pinzauti. The influence of the wind on nectar secretion from the melon and on the flight of bees: the use of an artificial wind-break, Apidologie, 1986, 17 (1), pp.63-72). C. Brittain, C. Kremen e A.-M. Klein osservano che con venti superiori a 2.5 m/s le api visitano i fiori meno frequentemente e raccolgono solo dai rami più bassi degli alberi (Biodiversity buffers pollination from changes in environmental conditions. Glob Change Biol 19:540–547); più in generale, il vento rende più difficoltoso il volo, sia direttamente spingendo le api fuori rotta che indirettamente muovendo gli ostacoli sul percorso,e forza le api ad adottare strategie compensative (Nicholas P. Burnett, Marc A. Badger, Stacey A. Combes, Wind and obstacle motion affect honeybee flight strategies in cluttered environments, Journal of Experimental Biology (2020) 223 (14): jeb222471.Per una ricca rassegna della letteratura in proposito si veda Csilla Vincze, Ádám Leelőssy, Edit Zajácz, Róbert Mészáros, A review of short‑term weather impacts on honey production International Journal of Biometeorology (2025) 69:303–317.
[6] Vedi i lavori di Hennessy e colleghi citati nella nota precedente.
[11] Daniele Alberoni, Luca Bosco e Enrico Ercole, Flussi nettariferi: complessità, L'Apis, dossier allegato al n° 9, 2021. Il tema, inclusa un'anticipazione della ricerca i questione, è stato presentato alla conferenza dal medesimo titolo tenuta da Daniele Alberoni, Chiara Braglia e Zed Nabulsi il 14 febbriaio 2025 a Bellinzona.
Appendice: i risultati delle modellistiche
Arnia 10, deviazioni dalla parabola in funzione di: velocità max giornaliera del vento, mm pioggia, luce solare, minuti in cui l'umidità assoluta supera 15 g/m3:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | −0.324459 | 0.591346 | −0.5487 | 0.59 | |
|
vento_velocitADailyMax
|
−0.498790 | 0.110798 | −4.502 | 0.0003 | *** |
| pioggia | 0.0413795 | 0.0118811 | 3.483 | 0.0027 | *** |
| luce_solare | 9.45E-08 | 2.83E-08 | 3.337 | 0.0037 | *** |
| AHa15 | 0.000672629 | 0.000250026 | 2.69 | 0.015 | ** |
|
Media var. dipendente
|
−0.035177 |
SQM var. dipendente
|
0.58999 | ||
|
Somma quadr. residui
|
2.397778 |
E.S. della regressione
|
0.364979 | ||
| R-quadro | 0.68689 |
R-quadro corretto
|
0.61731 | ||
| F(4, 18) | 9.871953 | P-value(F) | 0.000208 | ||
|
Log-verosimiglianza
|
−6.634642 | Criterio di Akaike | 23.26928 | ||
|
Criterio di Schwarz
|
28.94675 | Hannan-Quinn | 24.69715 | ||
| rho | 0.121208 | Durbin-Watson | 1.696722 |
Arnia 23, deviazioni dalla media degli inviluppi in funzione di: velocità max giornaliera del vento, mm pioggia, luce solare, minuti in cui la temperatura esterna supera 25°C:
| Coefficiente | Errore Std. | rapporto t | p-value | sigificatività | |
| const | −0.252427 | 0.637923 | −0.3957 | 0.697 | |
| pioggia | 0.0507541 | 0.0154595 | 3.283 | 0.0041 | *** |
| luce_solare | 1.13E-07 | 3.38E-08 | 3.341 | 0.0036 | *** |
|
vento_velocitADailyMax
|
−0.668814 | 0.13517 | −4.948 | 0.0001 | *** |
| MinutesText25A | 0.0013421 | 0.000640833 | 2.094 | 0.0507 | * |
|
Media var. dipendente
|
0.13645 |
SQM var. dipendente
|
0.738872 | ||
|
Somma quadr. residui
|
3.67143 |
E.S. della regressione
|
0.451629 | ||
| R-quadro | 0.694315 |
R-quadro corretto
|
0.626385 | ||
| F(4, 18) | 10.22104 | P-value(F) | 0.000169 | ||
|
Log-verosimiglianza
|
−11.53409 | Criterio di Akaike | 33.06817 | ||
|
Criterio di Schwarz
|
38.74565 | Hannan-Quinn | 34.49604 | ||
| rho | −0.029180 | Durbin-Watson | 2.01053 |
Nota: in questo modello l'inserimento di umidità assoluta, temperatura o umidità relativa non produce risultati significativi.
Arnia 36, deviazioni dalla parabola in funzione di: velocità max giornaliera del vento, mm pioggia, luce solare, minuti in cui l'umidità assoluta nelle ore diurne supera 15 g/m3:
| Coefficiente | Errore Std. | rapporto t | p-value | significatività | |
| const | −0.801327 | 0.901273 | −0.8891 | 0.3857 | |
|
radiazionesolaregiornali_aaa
|
0.127802 | 0.0341789 | 3.739 | 0.0015 | *** |
|
vento_velocitADailyMax
|
−0.771054 | 0.153105 | −5.036 | <0.0001 | *** |
|
minutipioggiadaytime
|
0.0212253 | 0.00585505 | 3.625 | 0.0019 | *** |
|
AHlareger15daytime
|
0.00118202 | 0.000438992 | 2.693 | 0.0149 | ** |
|
Media var. dipendente
|
−0.026621 |
SQM var. dipendente
|
0.873082 | ||
|
Somma quadr. residui
|
4.233578 |
E.S. della regressione
|
0.484973 | ||
| R-quadro | 0.74755 |
R-quadro corretto
|
0.69145 | ||
| F(4, 18) | 13.32532 | P-value(F) | 0.000032 | ||
|
Log-verosimiglianza
|
−13.17245 | Criterio di Akaike | 36.3449 | ||
|
Criterio di Schwarz
|
42.02237 | Hannan-Quinn | 37.77277 | ||
| rho | 0.091259 | Durbin-Watson | 1.776596 |
Arnia 39, deviazioni dalla parabola in funzione di: velocità max giornaliera del vento, mm pioggia, luce solare, minuti in cui l'umidità assoluta supera 15 g/m3:
| Coefficiente | Errore Std. | rapporto t | p-value | significatività | |
| const | −0.520679 | 0.546992 | −0.9519 | 0.3538 | |
|
vento_velocitADailyMax
|
−0.348136 | 0.102487 | −3.397 | 0.0032 | *** |
| pioggia | 0.0442315 | 0.01099 | 4.025 | 0.0008 | *** |
| luce_solare | 8.36E-08 | 2.62E-08 | 3.194 | 0.005 | *** |
| AHa15 | 0.000463291 | 0.000231272 | 2.003 | 0.0604 | * |
|
Media var. dipendente
|
−0.015736 |
SQM var. dipendente
|
0.492222 | ||
|
Somma quadr. residui
|
2.051576 |
E.S. della regressione
|
0.337604 | ||
| R-quadro | 0.615105 |
R-quadro corretto
|
0.529572 | ||
| F(4, 18) | 7.191491 | P-value(F) | 0.001212 | ||
|
Log-verosimiglianza
|
−4.841400 | Criterio di Akaike | 19.6828 | ||
|
Criterio di Schwarz
|
25.36027 | Hannan-Quinn | 21.11067 | ||
| rho | −0.043781 | Durbin-Watson | 2.016987 |
Arnia Jolly, deviazioni dalla parabola in funzione di: velocità max giornaliera del vento, mm pioggia, luce solare, minuti in cui l'umidità assoluta supera 15 g/m3:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | −0.642928 | 0.737456 | −0.8718 | 0.3948 | |
|
vento_velocitADailyMax
|
−0.363859 | 0.138173 | −2.633 | 0.0169 | ** |
| pioggia | 0.0278096 | 0.0148167 | 1.877 | 0.0768 | * |
| luce_solare | 8.92E-08 | 3.53E-08 | 2.525 | 0.0212 | ** |
| AHa15 | 0.000857656 | 0.000311802 | 2.751 | 0.0132 | ** |
|
Media var. dipendente
|
−0.012005 |
SQM var. dipendente
|
0.599765 | ||
|
Somma quadr. residui
|
3.729045 |
E.S. della regressione
|
0.455158 | ||
| R-quadro | 0.528792 |
R-quadro corretto
|
0.424079 | ||
| F(4, 18) | 5.049925 | P-value(F) | 0.006596 | ||
|
Log-verosimiglianza
|
−11.71315 | Criterio di Akaike | 33.42631 | ||
|
Criterio di Schwarz
|
39.10378 | Hannan-Quinn | 34.85417 | ||
| rho | −0.001939 | Durbin-Watson | 1.936669 |
Arnia 10, raccolto giornaliero netto in funzione di: velocità max giornaliera del vento, minuti in cui la temperatura esterna supera 27°C:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | 2.32649 | 0.773555 | 3.008 | 0.007 | *** |
|
vento_velocitADailyMax
|
−0.635628 | 0.243449 | −2.611 | 0.0167 | ** |
| MinutesText27 | 0.00224774 | 0.0010467 | 2.147 | 0.0442 | ** |
|
Media var. dipendente
|
1.093023 |
SQM var. dipendente
|
0.996117 | ||
|
Somma quadr. residui
|
14.17791 |
E.S. della regressione
|
0.841959 | ||
| R-quadro | 0.350516 |
R-quadro corretto
|
0.285567 | ||
| F(2, 20) | 5.396836 | P-value(F) | 0.013356 | ||
|
Log-verosimiglianza
|
−27.07178 | Criterio di Akaike | 60.14357 | ||
|
Criterio di Schwarz
|
63.55005 | Hannan-Quinn | 61.00029 | ||
| rho | 0.592376 | Durbin-Watson | 0.841061 | ||
Nota: l'inserimento di altre variabili (pioggia, luminosità, umidità relativa o assoluta) non produce risultati significati per nessuna di queste variabili
Arnia 23, raccolto giornaliero netto in funzione di: velocità max giornaliera del vento, minuti in cui la temperatura esterna supera 25°C:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | 3.07807 | 0.98935 | 3.111 | 0.0055 | *** |
|
vento_velocitADailyMax
|
−0.792955 | 0.28717 | −2.761 | 0.012 | ** |
| MinutesText25A | 0.00305712 | 0.00120077 | 2.546 | 0.0192 | ** |
|
Media var. dipendente
|
1.938395 |
SQM var. dipendente
|
1.243515 | ||
|
Somma quadr. residui
|
19.79209 |
E.S. della regressione
|
0.994789 | ||
| R-quadro | 0.418209 |
R-quadro corretto
|
0.36003 | ||
| F(2, 20) | 7.1883 | P-value(F) | 0.004443 | ||
|
Log-verosimiglianza
|
−30.90815 | Criterio di Akaike | 67.8163 | ||
|
Criterio di Schwarz
|
71.22279 | Hannan-Quinn | 68.67302 | ||
| rho | 0.526948 | Durbin-Watson | 0.92749 |
Queste sono le uniche variabili significative, con l'eccezione dei minuti a temperatura esterna > 26 o 27°C anziché 25°C, che producono un numero p più alto di quello in tabella
Arnia 36, raccolto giornaliero netto in funzione di: velocità max giornaliera del vento, minuti in cui la temperatura esterna supera 25°C:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | 3.39486 | 1.11466 | 3.046 | 0.0064 | *** |
|
vento_velocitADailyMax
|
−0.953859 | 0.323542 | −2.948 | 0.0079 | *** |
| MinutesText25A | 0.00314779 | 0.00135286 | 2.327 | 0.0306 | ** |
|
Media var. dipendente
|
1.819379 |
SQM var. dipendente
|
1.400867 | ||
|
Somma quadr. residui
|
25.12331 |
E.S. della regressione
|
1.120788 | ||
| R-quadro | 0.418084 |
R-quadro corretto
|
0.359892 | ||
| F(2, 20) | 7.184609 | P-value(F) | 0.004452 | ||
|
Log-verosimiglianza
|
−33.65106 | Criterio di Akaike | 73.30212 | ||
|
Criterio di Schwarz
|
76.7086 | Hannan-Quinn | 74.15884 | ||
| rho | 0.506683 | Durbin-Watson | 0.95341 |
Arnia 39, raccolto giornaliero netto in funzione di: velocità max giornaliera del vento, minuti in cui la temperatura esterna supera 27°C:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | 1.8401 | 0.617595 | 2.979 | 0.0074 | *** |
|
vento_velocitADailyMax
|
−0.423935 | 0.194366 | −2.181 | 0.0413 | ** |
| MinutesText27 | 0.00182146 | 0.000835669 | 2.18 | 0.0414 | ** |
|
Media var. dipendente
|
1.107264 |
SQM var. dipendente
|
0.771366 | ||
|
Somma quadr. residui
|
9.037288 |
E.S. della regressione
|
0.672209 | ||
| R-quadro | 0.30961 |
R-quadro corretto
|
0.240571 | ||
| F(2, 20) | 4.484567 | P-value(F) | 0.024601 | ||
|
Log-verosimiglianza
|
−21.89303 | Criterio di Akaike | 49.78607 | ||
|
Criterio di Schwarz
|
53.19255 | Hannan-Quinn | 50.64279 | ||
| rho | 0.358576 | Durbin-Watson | 1.203505 |
Arnia Jolly, raccolto giornaliero netto in funzione di: velocità max giornaliera del vento, minuti in cui la temperatura esterna supera 27°C:
| Coefficiente | Errore Std. | rapporto t | p-value | ||
| const | 2.21494 | 0.679466 | 3.26 | 0.0039 | *** |
| MinutesText27 | 0.00347398 | 0.000919387 | 3.779 | 0.0012 | *** |
|
vento_velocitADailyMax
|
−0.570910 | 0.213838 | −2.670 | 0.0147 | ** |
|
Media var. dipendente
|
1.512595 |
SQM var. dipendente
|
1.000525 | ||
|
Somma quadr. residui
|
10.93869 |
E.S. della regressione
|
0.73955 | ||
| R-quadro | 0.503308 |
R-quadro corretto
|
0.453639 | ||
| F(2, 20) | 10.13321 | P-value(F) | 0.000914 | ||
|
Log-verosimiglianza
|
−24.08893 | Criterio di Akaike | 54.17785 | ||
|
Criterio di Schwarz
|
57.58434 | Hannan-Quinn | 55.03458 | ||
| rho | 0.533086 | Durbin-Watson | 0.91391 |


















